KH_C++
노멀 매핑(Normal Mapping), 탄젠트 스페이스(Tangent Space) 본문
[ Normal Mapping ]
법선 매핑, 노멀 매핑(normal mapping)은 3차원 컴퓨터 그래픽스에서 튀어나온 곳과 움푹 틀어간 곳의 빛을 왜곡시키는 기법으로, 범프 매핑의 구현체이다. Dot3 bump mapping이라고도 한다. 더 많은 폴리곤을 사용하지 않고 세세한 부분을 추가하기 위해 사용한다.

단순해진 메시(mesh)를 더 자세하게 만들기 위해 사용되는 법선 매핑.
[ Tangent Space ]
지구본이 있다고 하자, 이걸 쫙 펼쳐 지도를 만들었다고 하자, 그런데 다시 지구본이 필요해서 지도를 다시 지구본으로 만들어야 한다고 했을 때, 어떻게 하면 지구본을 다시 만들 수 있을까? 쉬워보이지만 그런 단순한 문제는 아니다.
완벽하게 맞춰진 예는 아니지만 탄젠트 공간이 필요한 이유를 가장 잘 설명해주고있다.
만약 우리가 어떠한 3차원 물체를 2차원 평면으로 만들었다면, 우리는 이 2차원 평면을 바탕으로 3차원의 물체를 절대로 만들 수 없다.
하지만, 3차원 물체를 2차원 평면으로 변환할 때, 2차원 평면의 각 점에 그것이 3차원에서 가졌던 어떠한 정보를 저장해두었다면 어때,, 이렇게되면 우리는 어떻게든 2차원 평면을 다시 3차원 물체로 복원할 수 있게 될 것이다.
여기서 말하는 어떠한 정보가 바로 탄젠트 공간이다.
탄젠트 공간의 정의
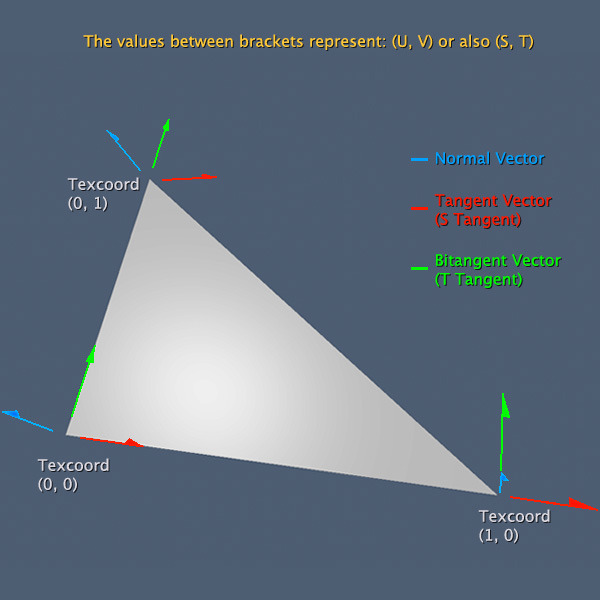
3차원 공간의 탄젠트 공간은 다음의 세 벡터를 축으로 하는 공간이다.
1) 한 점의 법선 벡터 // Normal(N)
2) 한 점의 접선(탄젠트) 벡터 // Tangent(T)
3) 바이노멀 벡터 : 법선 벡터와 접선 벡터를 외적하면 구할 수 있는 벡터 // Binomal(B)
일반적으로 탄젠트 공간은 원래의 공간과 같은 차원을 가지며, 한 점에서 생성 가능한 모든 접선 벡터를 포함한다.
위 그림의 경우엔 접선 벡터와 바이노멀 벡터가 생성하는 평면은 가능한 모든 접선 벡터를 포함한다.
주의할 점은 탄젠트 공간의 개념은 비단 3차원 공간만이 아닌 임의의 차원의 공간에 대해서도 적용할 수 있다는 점이다.
각 버텍스마다 B = N x T로 정의되고 이 세 벡터를 축(Axes)으로 갖는 공간을 탄젠트 공간라고 한다.
노말맵, 범프맵 등의 텍스쳐는 탄젠트 공간를 기준 좌표로 갖고 라이트 벡터 등은 Object Space를 기준 좌표로 갖기 때문에 같은 공간 기준 좌표로 맞춰 줘야 한다.
Tangent(Local) Space <==> Object(World) Space
Object-to-Tangent Matrix = [ Tx Ty Tz ]
[ Bx By Bz ]
[ Nx Ny Nz ]
Tangent Space를 Object Space로 변환하기 위해서는 위 행렬의 역행렬이 필요하다.
(매 픽셀마다 변환 연산을 해 주어야 함)
그러나 구할 필요가 없다 => 하나의 회전 행렬과 같음. 회전 행렬의 역행렬은 Transposed Matrix인데
전치 행렬도 구할 필요 없다 => 행렬을 곱해주는 순서만 바꾸어 주면 된다.
출처:
https://www.wikiwand.com/ko/%EB%B2%95%EC%84%A0_%EB%A7%A4%ED%95%91
https://okayhere.tistory.com/54
https://wonjayk.tistory.com/91
'공부' 카테고리의 다른 글
| 포워드 렌더링(Forward Rendering), 디퍼드 렌더링(Deferred Rendering) (0) | 2023.06.28 |
|---|---|
| 그림자 매핑(Shadow Mapping) (0) | 2023.06.26 |
| 스키닝(Skinning) (0) | 2023.06.23 |
| SIMD (Single Instruction Multiple Data) (0) | 2023.06.20 |
| Ambient, Diffuse, Specular, Phong Reflection (1) | 2023.06.07 |



